Experiment 2.9.1: Delete only red with two repulsive regularizers

This is a re-run of Ex 2.9 with more mature tooling. See the earlier notebook for discussion. Unlike 2.9, we only use one label (red), but unlike 2.10.1, we use both an anti-subspace and anti-anchor regularizer.

from __future__ import annotations

nbid = '2.9.1'  # ID for tagging assets
nbname = 'Ablate red (only), 5D'
experiment_name = f'Ex {nbid}: {nbname}'
project = 'ex-preppy'

# Basic setup: Logging, Experiment (Modal)
import logging

import modal

from infra.requirements import uv_freeze, project_packages
from utils.logging import SimpleLoggingConfig
from ex_color.vis import NbViz

logging_config = (
    SimpleLoggingConfig()
    .info('notebook', 'utils', 'mini', 'ex_color')
    .error('matplotlib.axes')  # Silence warnings about set_aspect
)
logging_config.apply()

# This is the logger for this notebook
log = logging.getLogger(f'notebook.{nbid}')

image = (
    modal.Image.debian_slim()
    .pip_install(*uv_freeze(all_groups=True, not_groups='dev'))
    .add_local_python_source(*project_packages())
)
volume = modal.Volume.from_name(f'{project}-{nbid}', create_if_missing=True, version=2)
app = modal.App(name=f'{project}-{nbid}', image=image, volumes={'/data': volume})

viz = NbViz(nbid)
None  # prevent auto-display of this cell

Model parameters

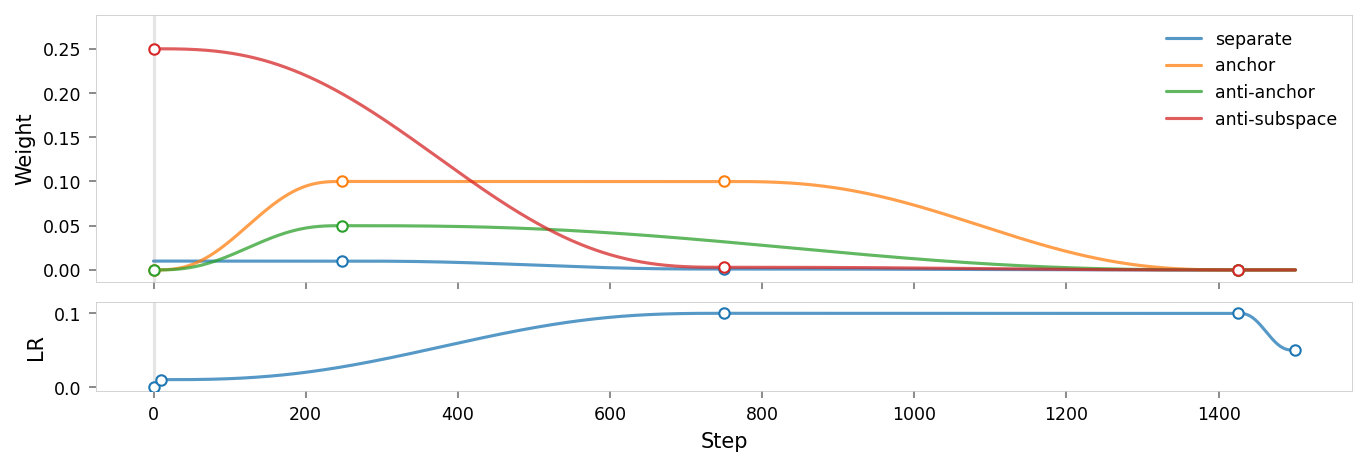
Like Ex 2.9, we use the following regularizers:

  • Anchor: pins red to $(1,0,0,0,0)$ (5D)
  • AxisAlignedSubspace: repels everything from dimension $1$ (with varying weight, see schedule)
  • Separate: angular repulsion to reduce global clumping (applied within each batch)

Since we're isolating red, we have 5D latent embeddings and two nonlinear activation functions in the encoder and decoder, to allow the latent space to be warped more.

But unlike 2.9:

  • Anti-anchor: has been removed, relying on anti-subspace to keep other concepts clear of the dimension to be ablated.
  • Unitarity: is present in this list, but we'll do a run without it too.
import torch

from ex_color.loss import AngularAnchor, AntiAnchor, AxisAlignedSubspace, Separate, RegularizerConfig

K = 5  # bottleneck dimensionality
N = 2  # number of nonlinear layers
H = 10  # hidden layer size
RED = (1, 0, 0, 0, 0)
ANTI_RED = (-1, 0, 0, 0, 0)
assert len(RED) == len(ANTI_RED) == K
BATCH_SIZE = 64
CUBE_SUBDIVISIONS = 8
NUM_RUNS = 60  # to probe seed sensitivity
RUN_SEEDS = [i for i in range(NUM_RUNS)]

reg_separate = RegularizerConfig(
    name='separate',
    compute_loss_term=Separate(power=100.0, shift=True),
    label_affinities=None,
    layer_affinities=['bottleneck'],
)
reg_anchor = RegularizerConfig(
    name='anchor',
    compute_loss_term=AngularAnchor(torch.tensor(RED, dtype=torch.float32)),
    label_affinities={'red': 1.0},
    layer_affinities=['bottleneck'],
    phase=('train', 'validate'),
)
reg_anti_anchor = RegularizerConfig(
    name='anti-anchor',
    compute_loss_term=AntiAnchor(torch.tensor(ANTI_RED, dtype=torch.float32)),
    label_affinities=None,
    layer_affinities=['bottleneck'],
    phase=('train', 'validate'),
)
reg_anti_subspace = RegularizerConfig(
    name='anti-subspace',
    compute_loss_term=AxisAlignedSubspace((0,), invert=True),
    label_affinities=None,
    layer_affinities=['bottleneck'],
)

from mini.temporal.dopesheet import Dopesheet

dopesheet = Dopesheet.from_csv(f'./ex-{nbid}-dopesheet.csv')
viz.tab_dopesheet(dopesheet)
viz.plot_dopesheet(dopesheet)

Parameter schedule

STEP PHASE ACTION lr separate anchor anti-anchor anti-subspace
0 Train 1e-08 0 0 0.25
10 0.01
248 0.01 0.1 0.05
750 0.1 0.001 0.1 0.003
1425 0.1 0 0 0 0
1500 0.05
Plot showing the parameter schedule for the training run, titled "". The plot has two sections: the upper section shows various regularization weights over time, and the lower section shows the learning rate over time. The x-axis represents training steps.

Data

Data is the same as last time: color cubes with values in RGB.

from torch.utils.data import DataLoader, RandomSampler

from ex_color.data.cube_dataset import prep_color_dataset, redness, stochastic_labels, exact_labels


def prep_train_data(training_subs: int, *, batch_size: int) -> DataLoader:
    dataset = prep_color_dataset(
        training_subs,
        sample_at='cell-corners',
        red=lambda c: redness(c) ** 8 * 0.08,
    )
    return DataLoader(
        dataset,
        batch_size=batch_size,
        num_workers=4,
        sampler=RandomSampler(dataset, num_samples=len(dataset), replacement=True),
        collate_fn=stochastic_labels,
    )


def prep_val_data(training_subs: int, *, batch_size: int) -> DataLoader:
    dataset = prep_color_dataset(
        training_subs,
        sample_at='cell-centers',
        red=lambda c: redness(c) == 1,
    )
    return DataLoader(
        dataset,
        batch_size=batch_size,
        num_workers=2,
        collate_fn=exact_labels,
    )

Train

from typing import Callable

import torch
import wandb

from ex_color.model import CNColorMLP
from ex_color.seed import set_deterministic_mode
from ex_color.workflow import train_model
from ex_color.evaluation import Result
from utils.time import hour


@app.function(
    cpu=1,
    max_containers=20,
    timeout=1 * hour,
    env={'WANDB_API_KEY': wandb.Api().api_key or ''},
)
async def train(
    dopesheet: Dopesheet,
    regularizers: list[RegularizerConfig],
    *,
    seed: int,
    score_fn: Callable[[CNColorMLP], float],
):
    """Train the model with the given dopesheet and variant."""
    logging_config.apply()

    if seed is not None:
        set_deterministic_mode(seed)

    train_loader = prep_train_data(CUBE_SUBDIVISIONS, batch_size=BATCH_SIZE)
    val_loader = prep_val_data(CUBE_SUBDIVISIONS, batch_size=BATCH_SIZE)
    model = CNColorMLP(K, n_nonlinear=N)
    res = train_model(
        model,
        dopesheet,
        regularizers,
        train_loader,
        val_loader,
        experiment_name=experiment_name,
        project=project,
        hparams={'seed': seed},
    )

    score = score_fn(res.model)
    key = f'model-{res.id_}.pt'
    torch.save(res.model.state_dict(), f'/data/{key}')
    return Result(seed, key, res.url, res.summary, score)

from ex_color.evaluation import EvaluationPlan, ScoreByHSVSimilarity
from ex_color.surgery import ablate

ablation_plan = EvaluationPlan(
    {'ablated'},
    lambda m: ablate(m, 'bottleneck', [0]),
    [],
)

score_fn = ScoreByHSVSimilarity(ablation_plan, (0.0, 1.0, 1.0), power=3.0, cube_subdivisions=CUBE_SUBDIVISIONS)

import asyncio

# Reload dopesheet: makes tweaking params during development easier
dopesheet = Dopesheet.from_csv(f'./ex-{nbid}-dopesheet.csv')
regularizers = [reg_separate, reg_anchor, reg_anti_anchor, reg_anti_subspace]


async def sweep():
    logging_config.apply()
    workers = [train.remote.aio(dopesheet, regularizers, seed=seed, score_fn=score_fn) for seed in RUN_SEEDS]
    return await asyncio.gather(*workers)


with app.run():
    results = await sweep()

from IPython.display import display
from ex_color.evaluation import results_to_dataframe

runs_df = results_to_dataframe(results)
# Show min, max, mean, stddev of each column
log.info(f'Summary statistics for all {len(runs_df)} runs:')
display(runs_df.describe().loc[['min', 'max', 'mean', 'std']].style.format(precision=4))

print('Correlation of reconstruction error vs. similarity to anchor')
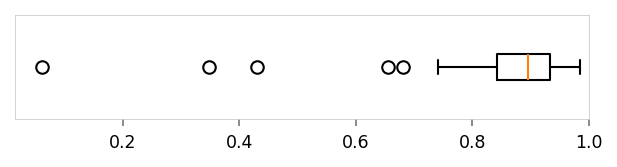
viz.plot_boxplot(runs_df['score'], ylabel='', xlim=(None, 1), tags=('score',))

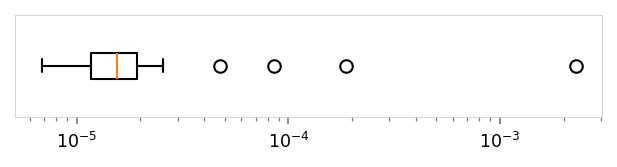
print('Reconstruction loss')
viz.plot_boxplot(runs_df['val_recon'], ylabel='', log_scale=True, tags=('val_recon',))

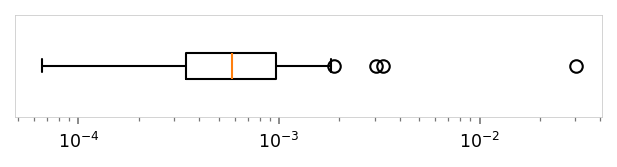
print('Anchor loss')
viz.plot_boxplot(runs_df['val_anchor'], ylabel='', log_scale=True, tags=('val_anchor',))

I 401.5 no.2.9.1:Summary statistics for all 60 runs:
  seed score val_recon val_anchor val_anti-anchor labels/n_total labels/n/_any labels/n/red val_loss _runtime
min 0.0000 0.0615 0.0000 0.0001 0.0000 96064.0000 68.0000 68.0000 0.0000 49.5294
max 59.0000 0.9848 0.0023 0.0302 0.0005 96064.0000 98.0000 98.0000 0.0023 189.6218
mean 29.5000 0.8570 0.0001 0.0012 0.0001 96064.0000 83.6167 83.6167 0.0001 89.6498
std 17.4642 0.1541 0.0003 0.0039 0.0001 0.0000 8.0087 8.0087 0.0003 42.3578 
Correlation of reconstruction error vs. similarity to anchor
Horizontal box plot showing the distribution of . 
Reconstruction loss
Horizontal box plot showing the distribution of . 
Anchor loss
Horizontal box plot showing the distribution of .

Select the best runs from the Pareto front of non-dominated runs, optimizing for both validation loss and score.

from ex_color.evaluation import pareto_front

non_dominated = pareto_front(runs_df, minimize=['val_recon', 'val_anchor', 'val_anti-anchor'], maximize=['score'])
log.info(f'Best of {len(non_dominated)} non-dominated runs (Pareto front):')
display(non_dominated.sort_values(by='score', ascending=False).head(5).style.format(precision=4, hyperlinks='html'))

I 403.6 no.2.9.1:Best of 22 non-dominated runs (Pareto front):
  seed wandb url score val_recon val_anchor val_anti-anchor labels/n_total labels/n/_any labels/n/red val_loss _runtime
33 33 https://wandb.ai/z0r/ex-preppy/runs/44c6iade 0.9848 0.0000 0.0033 0.0001 96064 75 75 0.0000 108.2703
45 45 https://wandb.ai/z0r/ex-preppy/runs/qypejhpg 0.9758 0.0000 0.0006 0.0000 96064 95 95 0.0000 52.1061
15 15 https://wandb.ai/z0r/ex-preppy/runs/qs71wem4 0.9715 0.0000 0.0011 0.0003 96064 85 85 0.0000 124.3796
28 28 https://wandb.ai/z0r/ex-preppy/runs/oso411l0 0.9704 0.0000 0.0005 0.0000 96064 94 94 0.0000 49.5294
9 9 https://wandb.ai/z0r/ex-preppy/runs/1whyclhd 0.9680 0.0000 0.0002 0.0002 96064 94 94 0.0000 102.4800 
from typing import cast

from mini.data import load_checkpoint_from_volume

best_run = results[cast(int, non_dominated['score'].idxmax())]
log.info(f'Loading checkpoint of best run: seed={best_run.seed}, score={best_run.score:.4f} @ {best_run.url}')
model = CNColorMLP(K, n_nonlinear=N)
model = load_checkpoint_from_volume(model, volume, best_run.checkpoint_key)

I 403.6 no.2.9.1:Loading checkpoint of best run: seed=33, score=0.9848 @ https://wandb.ai/z0r/ex-preppy/runs/44c6iade

Results

# # Generate a list of dimensions to visualize
# from itertools import combinations
# [
#     (
#         b,
#         a,
#         (a + 1) % 5 if (a + 1) % 5 not in (a, b) else (a + 2) % 5,
#     )
#     for a, b in combinations((0, 1, 2, 3, 4), 2)
# ]

from ex_color.evaluation import TestSet

test_set = TestSet.create()

from IPython.display import clear_output

baseline_results = test_set.evaluate(model, [], tags={'baseline'})
clear_output()

viz.plot_cube(baseline_results)
# viz.plot_recon_loss(baseline_results)
# viz.plot_latent_space(
#     baseline_results,
#     dims=[(1, 0, 2), (2, 0, 1), (3, 0, 1), (4, 1, 2), (3, 2, 4), (4, 3, 0)],
# )
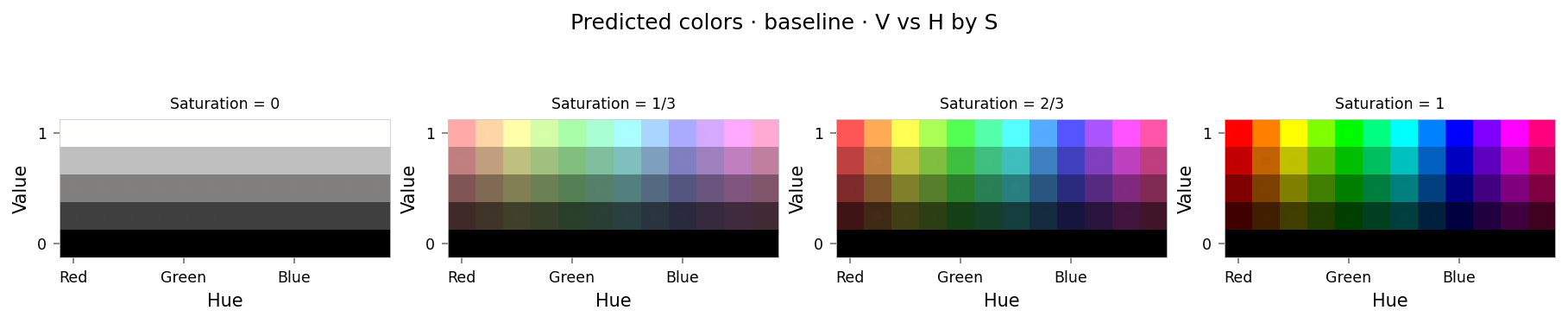
Plot showing four slices of the HSV cube, titled "Predicted colors · baseline · V vs H by S". Nominally, each slice has constant saturation, but varies in value (brightness) from top to bottom, and in hue from left to right. Each color value is represented as a square patch of that color. The outer portion of the patches shows the color as reconstructed by the model; the inner portion shows the true (input) color.

Ablation

from IPython.display import clear_output
from ex_color.surgery import ablate

ablated_model = ablate(model, 'bottleneck', [0])
ablation_results = test_set.evaluate(ablated_model, [], tags={'ablated'})
clear_output()

viz.plot_cube(ablation_results)
# viz.plot_recon_loss(ablation_results)
# viz.plot_latent_space(
#     ablation_results,
#     dims=[(1, 0, 2), (2, 0, 1), (3, 0, 1), (4, 1, 2), (3, 2, 4), (4, 3, 0)],
# )
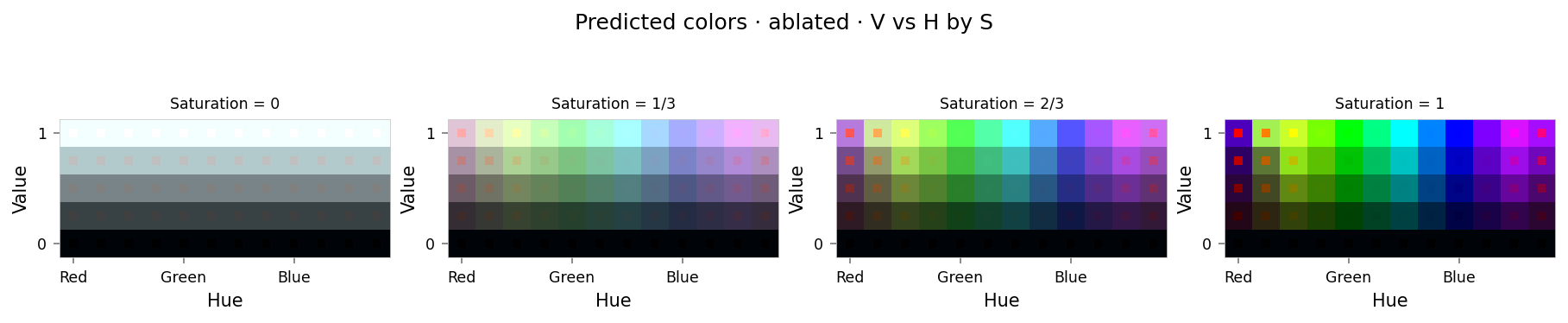
Plot showing four slices of the HSV cube, titled "Predicted colors · ablated · V vs H by S". Nominally, each slice has constant saturation, but varies in value (brightness) from top to bottom, and in hue from left to right. Each color value is represented as a square patch of that color. The outer portion of the patches shows the color as reconstructed by the model; the inner portion shows the true (input) color.

Pruning

from IPython.display import clear_output

from ex_color.surgery import prune

pruned_model = prune(model, 'bottleneck', [0])
pruned_results = test_set.evaluate(pruned_model, [], tags={'pruned'})
clear_output()

viz.plot_cube(pruned_results)
# viz.plot_recon_loss(pruned_results)
# viz.plot_latent_space(
#     pruned_results,
#     dims=[(0, None, 1), (1, None, 0), (2, None, 0), (3, 0, 1), (2, 1, 3), (3, 2, None)],
# )
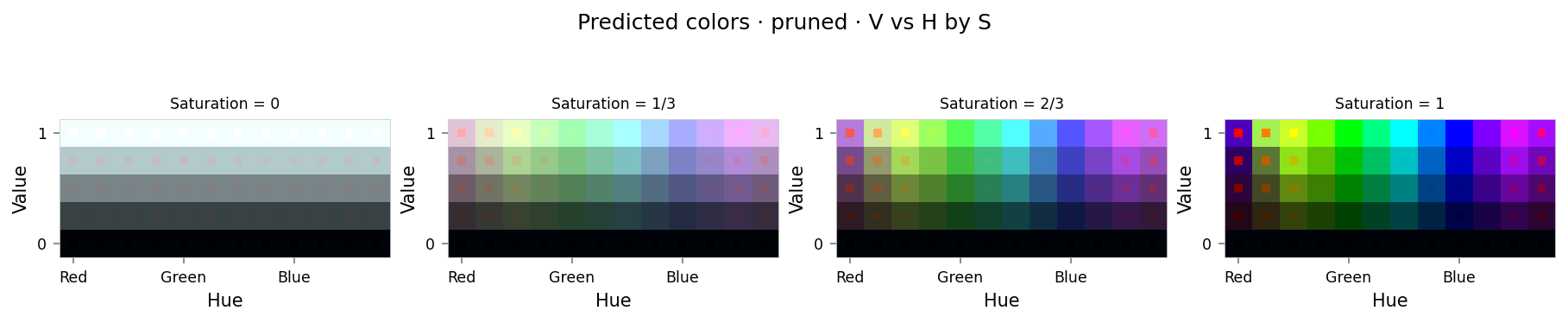
Plot showing four slices of the HSV cube, titled "Predicted colors · pruned · V vs H by S". Nominally, each slice has constant saturation, but varies in value (brightness) from top to bottom, and in hue from left to right. Each color value is represented as a square patch of that color. The outer portion of the patches shows the color as reconstructed by the model; the inner portion shows the true (input) color.

Suppression

Included for comparison/completeness, but this model was not really designed for it.

from math import cos, radians
from IPython.display import clear_output

from ex_color.intervention import Suppression, BoundedFalloff, InterventionConfig


falloff = BoundedFalloff(
    cos(radians(90)),  # cos(max_angle)
    1,  # completely squash fully-aligned vectors
    # 2,  # soft rim, sharp hub
    0,
)
suppression = InterventionConfig(
    apply=Suppression(torch.tensor(RED), falloff),
    layer_affinities=['bottleneck'],
)
suppression_results = test_set.evaluate(model, [suppression], tags={'suppression'})
clear_output()

viz.plot_cube(suppression_results)
# viz.plot_recon_loss(suppression_results)
# viz.plot_latent_space(
#     suppression_results,
#     dims=[(1, 0, 2), (2, 0, 1), (3, 0, 1), (4, 1, 2), (3, 2, 4), (4, 3, 0)],
# )
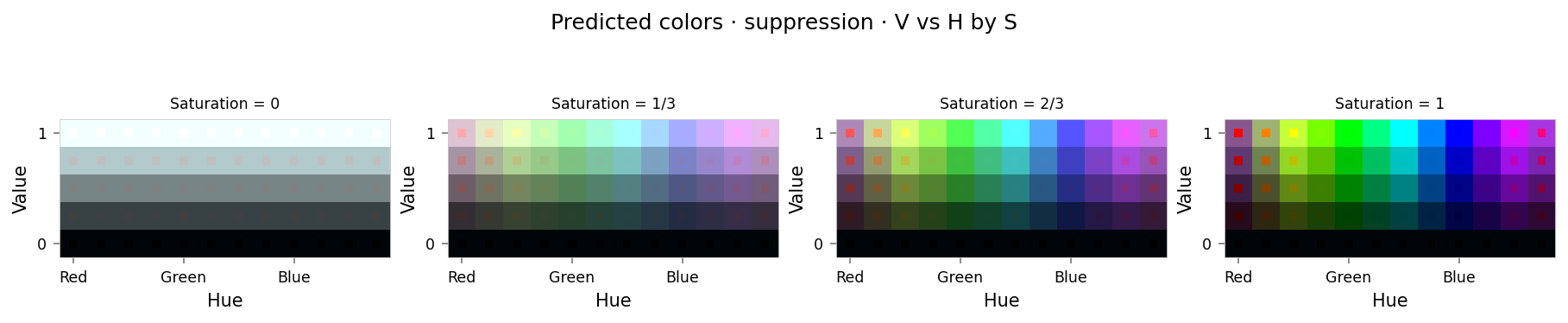
Plot showing four slices of the HSV cube, titled "Predicted colors · suppression · V vs H by S". Nominally, each slice has constant saturation, but varies in value (brightness) from top to bottom, and in hue from left to right. Each color value is represented as a square patch of that color. The outer portion of the patches shows the color as reconstructed by the model; the inner portion shows the true (input) color. 
import numpy as np
from ex_color.vis.helpers import ThemedAnnotation


max_error = np.max(
    [
        baseline_results.loss_cube['MSE'],
        ablation_results.loss_cube['MSE'],
        pruned_results.loss_cube['MSE'],
    ]
)

dims = ((3, 0, 1), (1, 2, 0))
pruned_dims = ((2, None, 0), (0, 1, None))

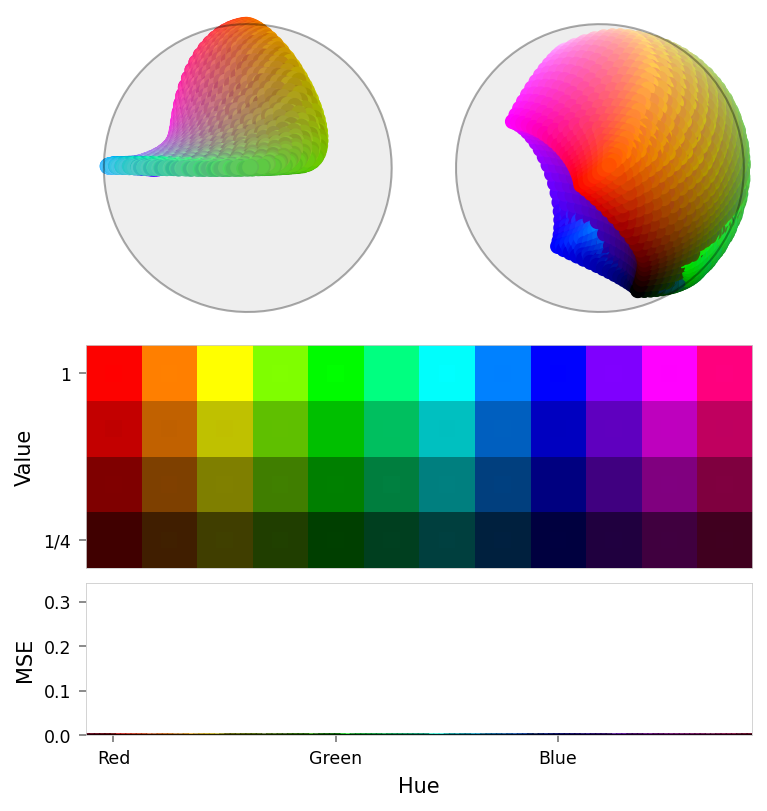
print('Baseline')
viz.plot_stacked_results(
    baseline_results,
    latent_dims=dims,
    max_error=max_error,
)

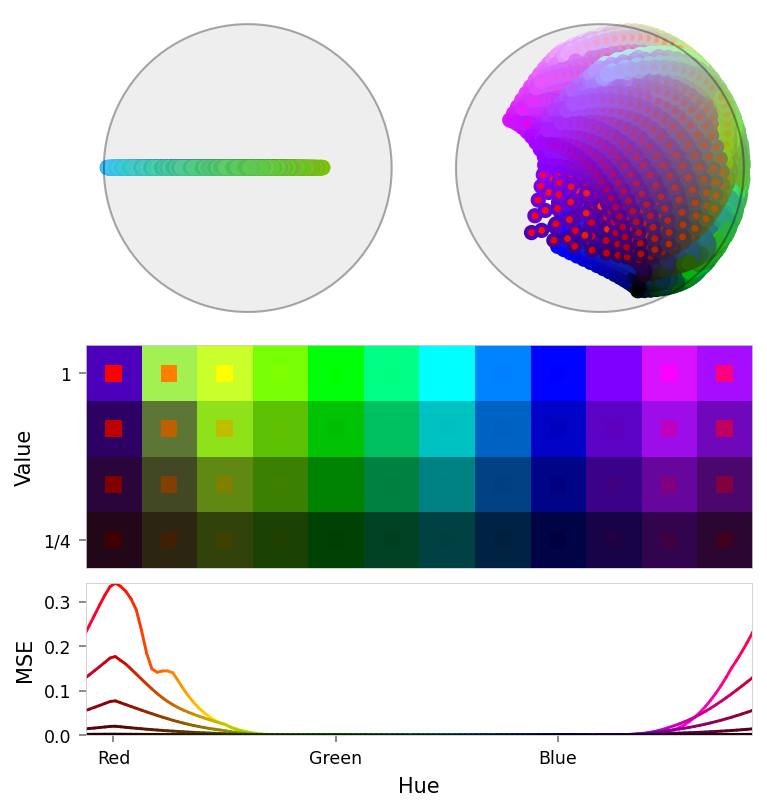
print('Ablation')
viz.plot_stacked_results(
    ablation_results,
    latent_dims=dims,
    max_error=max_error,
)

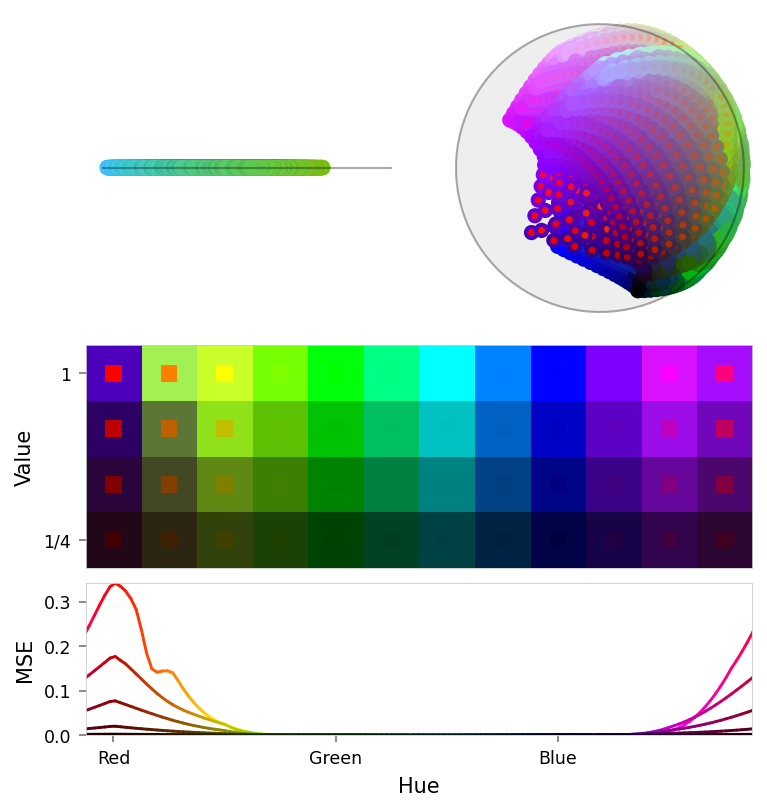
print('Pruned')
viz.plot_stacked_results(
    pruned_results,
    latent_dims=pruned_dims,
    max_error=max_error,
)

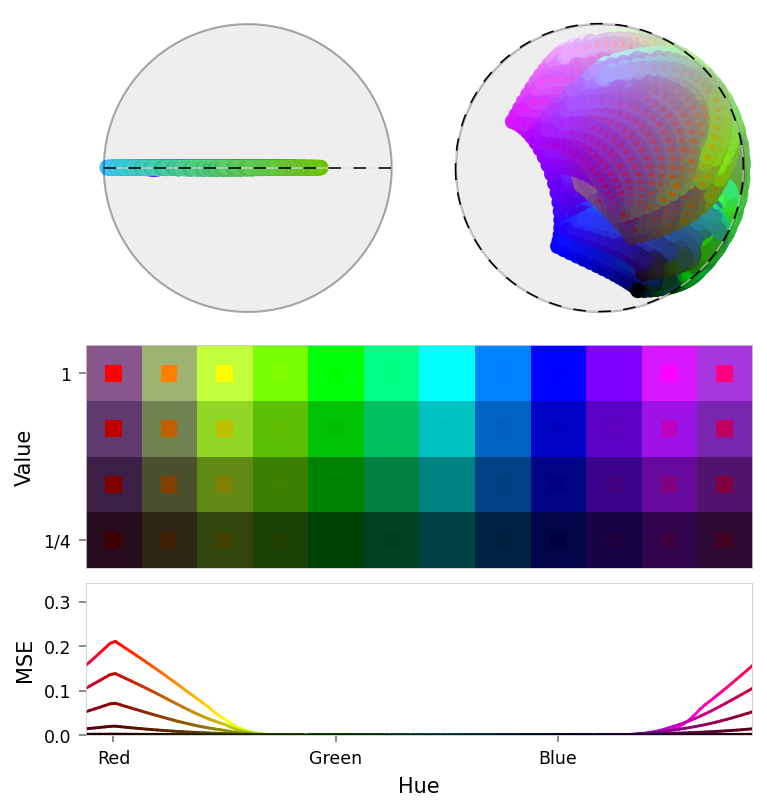
print('Suppression')
viz.plot_stacked_results(
    suppression_results,
    latent_dims=dims,
    max_error=max_error,
    latent_annotations=[
        ThemedAnnotation(direction=RED, angle=2 * (np.pi / 2 - falloff.a), dashed=True),
    ],
)

Baseline
Composite figure with two latent panels (top), a color slice (middle), and a loss chart (bottom). 
Ablation
Composite figure with two latent panels (top), a color slice (middle), and a loss chart (bottom). 
Pruned
Composite figure with two latent panels (top), a color slice (middle), and a loss chart (bottom). 
Suppression
Composite figure with two latent panels (top), a color slice (middle), and a loss chart (bottom). 
viz.tab_error_vs_color(baseline_results, ablation_results, pruned_results, suppression_results)
viz.tab_error_vs_color_latex(baseline_results, ablation_results, pruned_results, suppression_results)
Name RGB Baseline Ablated Δ Abl Pruned Δ Pru Suppression Δ Sup
red
0.000 0.343 +0.343 0.343 +0.343 0.213 +0.213
orange
0.000 0.143 +0.143 0.143 +0.143 0.128 +0.128
yellow
0.000 0.024 +0.024 0.024 +0.024 0.036 +0.036
lime
0.000 0.000 +0.000 0.000 +0.000 0.000 +0.000
green
0.000 0.001 +0.001 0.001 +0.001 0.001 +0.001
teal
0.000 0.000 +0.000 0.000 +0.000 0.000 +0.000
cyan
0.000 0.000 -0.000 0.000 -0.000 0.000 -0.000
azure
0.000 0.000 +0.000 0.000 +0.000 0.000 +0.000
blue
0.000 0.000 +0.000 0.000 +0.000 0.000 +0.000
purple
0.000 0.000 +0.000 0.000 +0.000 0.000 +0.000
magenta
0.000 0.009 +0.009 0.009 +0.009 0.011 +0.011
pink
0.000 0.124 +0.124 0.124 +0.124 0.103 +0.103
black
0.000 0.001 +0.001 0.001 +0.001 0.001 +0.001
dark gray
0.000 0.000 +0.000 0.000 +0.000 0.000 +0.000
gray
0.000 0.001 +0.001 0.001 +0.001 0.001 +0.001
light gray
0.000 0.002 +0.002 0.002 +0.002 0.002 +0.002
white
0.000 0.001 +0.001 0.001 +0.001 0.001 +0.001 
\begin{table}
\centering
\label{tab:placeholder}
\caption{Reconstruction error by color and intervention method}
\sisetup{
    round-mode = places,
    round-precision = 3,
    table-auto-round = true,
    % drop-zero-decimal = true,
}
\begin{tabular}{l c g g g g}
\toprule
\multicolumn{2}{c}{{Color}} & \multicolumn{1}{c}{{Baseline}} & \multicolumn{1}{c}{{Ab}} & \multicolumn{1}{c}{{Prun}} & \multicolumn{1}{c}{{Suppression}} \\
\midrule
Red        & \swatch{FF0000} &  0.000064271 &  0.343180478 &  0.343180478 &  0.213169754 \\
Orange     & \swatch{FF7F00} &  0.000001609 &  0.143432498 &  0.143432498 &  0.127903447 \\
Yellow     & \swatch{FFFF00} &  0.000000000 &  0.024397219 &  0.024397219 &  0.036187626 \\
Lime       & \swatch{7FFF00} &  0.000002130 &  0.000427035 &  0.000427035 &  0.000435619 \\
Green      & \swatch{00FF00} &  0.000051003 &  0.000510316 &  0.000510316 &  0.000540676 \\
Teal       & \swatch{00FF7F} &  0.000004940 &  0.000167426 &  0.000167426 &  0.000167415 \\
Cyan       & \swatch{00FFFF} &  0.000028671 & -0.000028671 & -0.000028671 & -0.000028671 \\
Azure      & \swatch{007FFF} &  0.000016649 &  0.000081700 &  0.000081700 &  0.000081838 \\
Blue       & \swatch{0000FF} &  0.000035178 &  0.000045453 &  0.000045453 &  0.000045883 \\
Purple     & \swatch{7F00FF} &  0.000005335 &  0.000006142 &  0.000006142 &  0.000006121 \\
Magenta    & \swatch{FF00FF} &  0.000016997 &  0.009266702 &  0.009266702 &  0.010696145 \\
Pink       & \swatch{FF007F} &  0.000005614 &  0.124145284 &  0.124145284 &  0.103091747 \\
Black      & \swatch{000000} &  0.000007270 &  0.000540850 &  0.000540850 &  0.000568996 \\
Dark gray  & \swatch{3F3F3F} &  0.000002058 &  0.000476244 &  0.000476244 &  0.000476932 \\
Gray       & \swatch{7F7F7F} &  0.000024290 &  0.000750420 &  0.000750420 &  0.000757260 \\
Light gray & \swatch{BFBFBF} &  0.000009449 &  0.002489201 &  0.002489201 &  0.002421958 \\
White      & \swatch{FFFFFF} &  0.000004127 &  0.000617128 &  0.000617128 &  0.000634405 \\
\bottomrule
\end{tabular}
\end{table}

viz.plot_error_vs_similarity(
    ablation_results,
    (0, 1, 1),
    anchor_name='red',
    power=3,
)

viz.plot_error_vs_similarity(
    pruned_results,
    (0, 1, 1),
    anchor_name='red',
    power=3,
)

viz.plot_error_vs_similarity(
    suppression_results,
    (0, 1, 1),
    anchor_name='red',
    power=2,
)
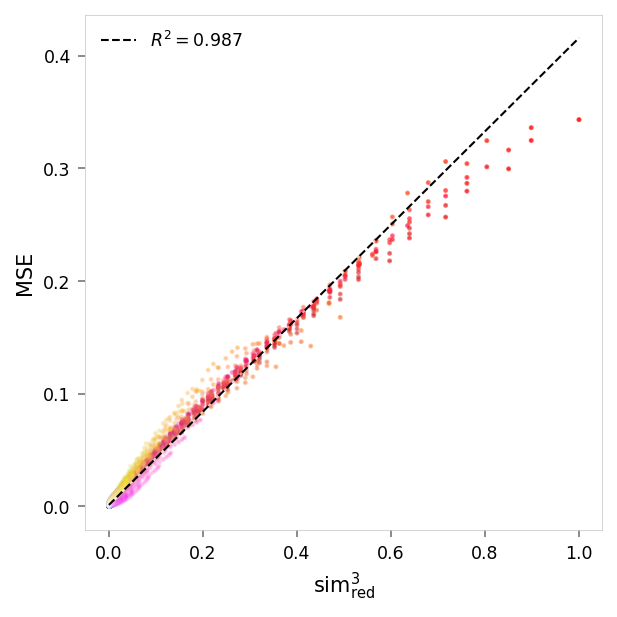
Scatter plot showing reconstruction error versus similarity to red. Each point represents a color, with its position on the x-axis indicating how similar it is to pure red, and its position on the y-axis indicating the reconstruction error (mean squared error) for that color. The points are colored according to their actual color values. 
MSE,sim³ ablated: r = 0.99, R²: 0.99, p = 0
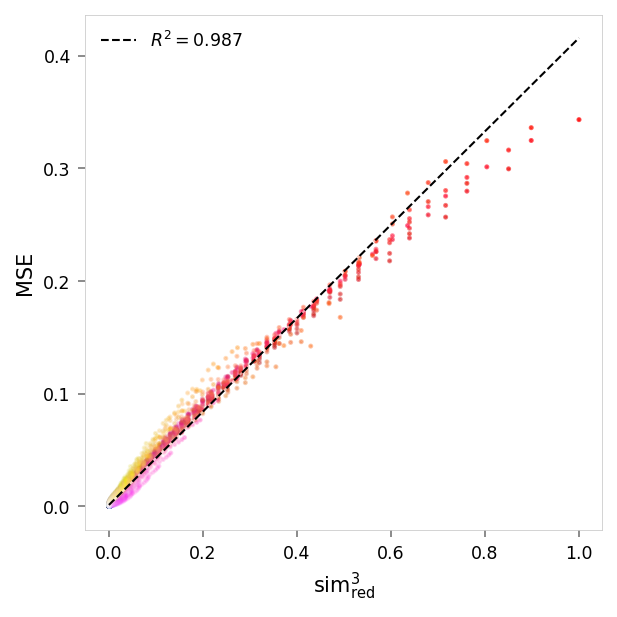
Scatter plot showing reconstruction error versus similarity to red. Each point represents a color, with its position on the x-axis indicating how similar it is to pure red, and its position on the y-axis indicating the reconstruction error (mean squared error) for that color. The points are colored according to their actual color values. 
MSE,sim³ pruned: r = 0.99, R²: 0.99, p = 0
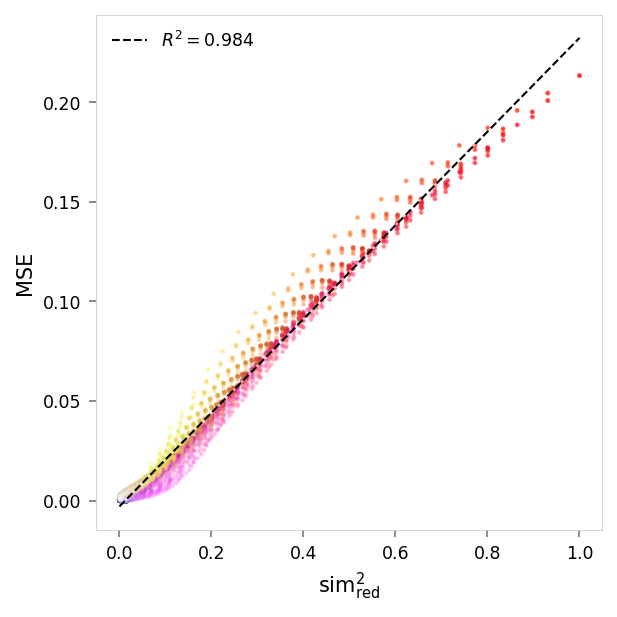
Scatter plot showing reconstruction error versus similarity to red. Each point represents a color, with its position on the x-axis indicating how similar it is to pure red, and its position on the y-axis indicating the reconstruction error (mean squared error) for that color. The points are colored according to their actual color values. 
MSE,sim² suppression: r = 0.99, R²: 0.98, p = 0