Experiment 2.1: Intervention lobes

In this series of experiments, we shall explore the effects of intervening on latent activations. Having structured the latent space (see Ex 1.7), it should just be a matter of transforming latent embeddings that are closely aligned to the anchored concepts.

We draw inspiration from shaders in computer graphics: BSDFs compute the output energy given: 1. an input light direction, and 2. the viewing direction, relative to the surface normal. Our interventions are similar: we have 1. a concept vector, and 2. activation vectors. If we treat the subject vector as analogous to a light source and acivation vectors as analogous to viewing directions, we may build on a wealth of established techniques.

Here we define our intervention as a BSDF-like function:

$$\alpha' = f(\mathbf{v},\alpha)$$

Where $\alpha$ is an embedding vector, $\mathbf{v}$ is the concept vector, and $\alpha'$ is the modified embedding. In fact $\mathbf{v}$ need not be a (directional) vector; it could be other geometric features of our embedding space, such as a subspace defined by multiple basis vectors. But for this experiment, we will limit ourselves to intervention on directions.

nb_id = '2.1'

Charting functions

from typing import Protocol, Sequence

import torch
from numpy.typing import NDArray
from torch import Tensor

from ex_color.intervention.intervention import ConstAnnotation, Intervention


def sample_idf(
    idf: Intervention, n=360, *, eps=0.0, include_end=False
) -> tuple[NDArray, NDArray, NDArray, tuple[str, NDArray]]:
    # Input angles θ_in: [0, 2π)
    thetas_in: Tensor = torch.linspace(eps, 2 * torch.pi - eps, steps=n + 1, dtype=torch.float32)
    if not include_end:
        thetas_in = thetas_in[:-1]

    # Unit circle directions, shape [n, 2]
    unit: Tensor = torch.stack((torch.cos(thetas_in), torch.sin(thetas_in)), dim=-1)

    # Apply intervention (idf expects Tensors); disable grad for safety
    with torch.no_grad():
        out: Tensor = idf(unit)  # [n, 2]
        annotation = idf.annotate_activations(unit)  # [n]

    # Convert outputs to polar coordinates
    y, x = out[..., 1], out[..., 0]
    theta_out = torch.atan2(y, x)  # [-π, π]
    # Wrap angles to be positive
    theta_out = (theta_out + 2 * torch.pi) % (2 * torch.pi)  # [0, 2π]
    r_out = torch.linalg.norm(out, dim=-1)

    return (
        theta_out.detach().cpu().numpy(),
        r_out.detach().cpu().numpy(),
        thetas_in.detach().cpu().numpy(),
        (annotation.name, annotation.values.detach().cpu().numpy()),
    )


class Mapper(Protocol):
    def __call__(self, alignment: Tensor) -> Tensor: ...

    @property
    def annotations(self) -> Sequence[ConstAnnotation]: ...

Special chart series (artists)

from math import radians

import numpy as np
from matplotlib.axes import Axes
from matplotlib.projections.polar import PolarAxes
from numpy.typing import NDArray
from torch import Tensor

from ex_color.intervention.intervention import Intervention

from typing import Literal
from matplotlib.patheffects import SimpleLineShadow, Normal


def wrapped_angular_diff(a: float, b: float) -> float:
    """Compute the angular difference between two angles a and b, wrapping around at 2π."""
    # Ensure 0 is considered close to 2pi
    diff = (b - a) % (2 * np.pi)
    return min(diff, 2 * np.pi - diff)


def filled_series(
    ax: Axes,
    xs: NDArray,
    ys: NDArray,
    *,
    color: str | None,
    alpha=0.3,
    close: Literal['auto', 'always'] = 'auto',
    shadow: bool,
    **kwargs,
):
    span_x = wrapped_angular_diff(xs[0], xs[-1])
    _close = close == 'always' or isinstance(ax, PolarAxes) and span_x < radians(2)

    ax.fill(
        np.concatenate([xs, [xs[0]]]) if _close else np.concatenate([[0], xs, [0]]),
        np.concatenate([ys, [ys[0]]]) if _close else np.concatenate([[0], ys, [0]]),
        color=color,
        alpha=alpha,
        zorder=0,
    )
    ax.plot(
        np.concatenate([xs, [xs[0]]]) if _close else xs,
        np.concatenate([ys, [ys[0]]]) if _close else ys,
        color=color,
        path_effects=[
            SimpleLineShadow((0, 0), linewidth=3, alpha=0.1),
            SimpleLineShadow((0, 0), linewidth=6, alpha=0.05),
            SimpleLineShadow((0, 0), linewidth=9, alpha=0.025),
            Normal(),
        ]
        if shadow
        else [],
        **kwargs,
    )


Shape = Literal['line', 'chord']


def diff_series(
    ax: Axes,
    xs1: NDArray,
    xs2: NDArray,
    ys1: NDArray,
    ys2: NDArray,
    *,
    shape: Shape,
    label: str | None = None,
    **kwargs,
):
    """Draw line segments between two series of points (xs1, ys1) and (xs2, ys2)."""
    # Split kwargs
    marker_kwargs = {k: v for k, v in kwargs.items() if k.startswith('marker')}
    other_kwargs = {k: v for k, v in kwargs.items() if not k.startswith('marker')}

    # Draw line segments between series 1 and 2
    for x1, x2, y1, y2 in zip(xs1, xs2, ys1, ys2, strict=True):
        if np.abs(x2 - x1) > np.pi:
            # Take the shortest path around the circle
            x1 += 2 * np.pi
        if shape == 'chord':
            # Draw a curve, like a chord diagram, to make it easier to see where the points go
            # Without this, rotations are hard to interpret because the lines have similar angles
            curve_length_x = wrapped_angular_diff(x1, x2)
            curve_power = 2.2
            curve_strength = 0.97 * (curve_length_x / np.pi) + 0.03
            xs = np.linspace(x1, x2, 100)
            ys = np.linspace(y1, y2, 100)
            # pull ys down in the middle
            yfrac = np.concatenate([np.linspace(1, 0, 50), np.linspace(0, 1, 50)])
            yfrac **= curve_power
            ys *= yfrac * curve_strength + 1 - curve_strength
        else:
            xs = [x1, x2]
            ys = [y1, y2]
        ax.plot(xs, ys, zorder=0, **other_kwargs)

    # Draw markers
    # # Starts
    # ax.plot(xs1, ys1, linestyle='', **marker_kwargs)
    # Ends
    ax.plot(xs2, ys2, linestyle='', **marker_kwargs)

    # Only add the label once
    if label:
        ax.plot([], [], label=label, **kwargs)

Polar lobe charts

These charts show a 2D slice of functions with a polar projection. This helps to visualize the shape of the intervention, although it's a bit hard to interpret the magnitude.

from itertools import cycle
from math import pi, acos

from utils.plt import Theme

NEON = ['hotpink', 'orange', 'limegreen', 'pink', 'aqua', 'yellow']


def draw_intervention_slice(ax: Axes | PolarAxes, idf: Intervention, *, theme: Theme):
    """
    Plot a 2D slice of an intervention function on a polar axes.

    The angular coordinate corresponds to the direction of a unit input vector.
    Two curves are drawn:
      - Transformed: the output vector converted to polar (θ_out, r_out)
      - Falloff: the magnitude of the intervention plotted against input θ

    Args:
        ax: A PolarAxes instance to draw into.
        idf: The intervention function to plot. Will be called with a tensor of [B,E] where E=2.
    """
    theta_out, r_out, thetas_in, annotation = sample_idf(idf, 360, eps=1e-7)

    # Post-intervention activations
    filled_series(
        ax,
        theta_out,
        r_out,
        color='#1f77b4',
        linewidth=2.0,
        label='Transformed',
        alpha=0.15 if isinstance(ax, PolarAxes) else 0.0,
        shadow=theme.val(False, dark=True),
    )

    # Magnitude of intervention
    filled_series(
        ax,
        thetas_in,
        annotation[1],
        color='#ff7f0e',
        close='always',
        linewidth=2.0,
        label=annotation[0],
        alpha=0.15 if isinstance(ax, PolarAxes) else 0.0,
        shadow=theme.val(False, dark=True),
    )

    # Differences
    theta_out, r_out, thetas_in, _ = sample_idf(idf, 360 // 10, eps=1e-7, include_end=idf.kind != 'linear')
    diff_series(
        ax,
        thetas_in,
        theta_out,
        np.ones_like(thetas_in),
        r_out,
        shape='line' if idf.kind == 'linear' else 'chord',
        color=theme.val('gray', light='black', dark='white'),
        alpha=0.6,
        linewidth=0.5,
        marker='o',
        markersize=2.0,
        markeredgecolor='none',
        markerfacecolor='white',
        label=r'Offset',
    )

    for annot, color in zip(idf.annotations, cycle(NEON), strict=False):
        if annot.kind == 'angular':
            cx = acos(annot.value)
            ax.axvline(cx, color=color, alpha=1.0, linewidth=1, linestyle='--', label=annot.name, zorder=0)
            ax.axvline(-cx, color=color, alpha=1.0, linewidth=1, linestyle='--', zorder=0)
        else:
            cy = annot.value
            ax.axhline(cy, color=color, alpha=1.0, linewidth=1, linestyle='--', label=annot.name, zorder=0)

    if isinstance(ax, PolarAxes):
        # Customize polar plot
        ax.set_theta_zero_location('N')  # 0° at top (perfect alignment)
        # ax.set_thetalim(0, np.pi)  # Only show 0 to π (hemisphere)

        # Configure polar grid
        ax.set_thetagrids([180], [''])  # One line: opposing (cos sim = -1)
        ax.set_rticks([0.0, 1.0])  # Just the outer circle

        # Set radial limit to comfortably contain all data and the unit radius
        max_r = max(r_out.max(), annotation[1].max(), 1.0)
        ax.set_rmax(max(1.0, max_r) * 1.1)

    else:
        ax.set_xlim(0, np.pi)
        ax.set_ylim(0, max(r_out.max(), annotation[1].max(), 1.0) * 1.1)

Linear charts

These charts show the effects of the intervention as well. The input to the intervention is the alignment with the concept vector — so we'll use that as the x-axis. The choice of y-axis depends on the type of the intervention:

• For suppression, it's useful to see the magnitude of the intervention
• For repulsion, it's more useful to see the output of the mapping (i.e. the post-intervention alignment).

# Helpers for linear charts reused across figures
from math import cos, pi, sqrt

from matplotlib.typing import ColorType
import numpy as np
import torch
from matplotlib.axes import Axes
from matplotlib.patheffects import SimpleLineShadow, Normal


def draw_mapping_linear(
    ax: Axes,
    mapping: Mapper,
    *,
    title: str | None = None,
    color: str = '#1f77b4',
    color_secondary: str = '#ff7f0e',
    show_identity: bool = True,
    theme: Theme,
) -> None:
    """
    Draw a linear mapping y = f(x) for cosine similarity inputs.

    x is cosine similarity in [-1, 1]. y is mapping(x) in [-1, 1].
    """
    x = np.linspace(-1, 1, 400, dtype=np.float32)
    xt = torch.from_numpy(x)
    with torch.no_grad():
        y = mapping(xt).detach().cpu().numpy()

    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    setup_cosine_axes(ax, axis='both')

    if show_identity:
        ax.axline((0, 0), slope=1, color='gray', alpha=0.2, linewidth=1, linestyle='--')

    # Fill region between identity and adjusted activations: this is the magnitude of the effect
    ax.fill_between(x, x, y, color=color_secondary, alpha=0.15, zorder=0)

    ax.plot(
        x,
        y,
        label=r'$m(\alpha)$',
        color=color,
        linewidth=2,
        path_effects=theme.val([], dark=[SimpleLineShadow((0, 0), linewidth=4, alpha=0.5), Normal()]),
    )

    for annot, _color in zip(mapping.annotations, cycle(NEON), strict=False):
        # Both axes are angular, so inspect direction
        if annot.direction == 'input':
            ax.axvline(annot.value, color=_color, alpha=1.0, linewidth=1, linestyle='--', label=annot.name, zorder=0)
            ax.text(
                annot.value + 0.02,
                ax.viewLim.ymin + 0.2,
                f'{annot.name} = {annot.value:.2g}',
                color=_color,
                fontsize='x-small',
                rotation=90,
            )
        else:
            ax.axhline(annot.value, color=_color, alpha=1.0, linewidth=1, linestyle='--', label=annot.name, zorder=0)
            ax.text(
                ax.viewLim.xmin + 0.2,
                annot.value + 0.02,
                f'{annot.name} = {annot.value:.2g}',
                color=_color,
                fontsize='x-small',
            )

    if title:
        ax.set_title(title)


def draw_suppression_strength(
    ax: Axes,
    falloff: Mapper,
    *,
    title: str | None = None,
    color: str = '#ff7f0e',
    color_secondary: str = '#1f77b4',
    theme: Theme,
) -> None:
    """
    Draw suppression amount vs cosine similarity.

    x: cosine similarity in [-1, 1]
    y: suppression amount in [0, 1] computed as falloff(alignment),
       where alignment = max(0, x) for unidirectional suppression.
    """
    x = np.linspace(-1, 1, 400, dtype=np.float32)
    alignment = np.clip(x, 0.0, 1.0).astype(np.float32)  # Only positive alignment contributes
    xt = torch.from_numpy(alignment)
    with torch.no_grad():
        y = falloff(xt).detach().cpu().numpy()

    ax.set_xlim(-1, 1)
    ax.set_ylim(0, max(1.0, float(np.max(y)) * 1.05))
    setup_cosine_axes(ax, axis='x')
    ax.set_ylabel(r'Suppression strength $g(\alpha)$', fontsize='small', labelpad=10)

    ax.plot(
        x,
        y,
        label=r'$g(\alpha)$',
        color=color,
        linewidth=2,
        path_effects=theme.val([], dark=[SimpleLineShadow((0, 0), linewidth=4, alpha=0.5), Normal()]),
    )

    # Threshold annotation for bounded falloffs defined over alignment

    for annot, _color in zip(falloff.annotations, cycle(NEON), strict=False):
        # One angular and one linear axis, so inspect type
        if annot.kind != 'linear':
            ax.axvline(annot.value, color=_color, alpha=1.0, linewidth=1, linestyle='--', label=annot.name, zorder=0)
            ax.text(
                annot.value + 0.02,
                ax.viewLim.ymin + 0.2,
                f'{annot.name} = {annot.value:.2g}',
                color=_color,
                fontsize='x-small',
                rotation=90,
            )
        else:
            ax.axhline(annot.value, color=_color, alpha=1.0, linewidth=1, linestyle='--', label=annot.name, zorder=0)
            ax.text(
                ax.viewLim.xmin + 0.2,
                annot.value + 0.02,
                f'{annot.name} = {annot.value:.2g}',
                color=_color,
                fontsize='x-small',
            )

    if title:
        ax.set_title(title)


def setup_cosine_axes(ax: Axes, axis: str = 'both') -> None:
    """
    Set cosine ticks/labels on axes for readability.

    axis: 'x' | 'y' | 'both'
    """
    # Major ticks at +-1, +-cos(30), +-cos(60), 0
    cos_values = np.array([-1, -cos(pi / 6), -cos(pi / 3), 0, cos(pi / 3), cos(pi / 6), 1.0])
    xlabels = np.array(['-1\nopposing', '', '', '0\northogonal', '', '', '1\naligned'])
    ylabels = np.array(['-1', '', '', '0', '', '', '1'])

    if axis in ('x', 'both'):
        ax.set_xticks(cos_values)
        ax.set_xticklabels(xlabels, fontsize='x-small')
        ax.set_xlabel(r'Alignment $\alpha = \mathbf{x} \cdot \mathbf{v}$', fontsize='small', labelpad=10)

    if axis in ('y', 'both'):
        ax.set_yticks(cos_values)
        ax.set_yticklabels(ylabels, fontsize='x-small')
        ax.set_ylabel(r'Output alignment $\alpha^\prime$', fontsize='small', labelpad=10)

    # Minor ticks at every 10 degrees
    cos_minor = np.cos(np.arange(0, 91, 10) * np.pi / 180)
    cos_minor = np.concatenate([-cos_minor[:-1], cos_minor])
    if axis in ('x', 'both'):
        ax.set_xticks(cos_minor, minor=True)
    if axis in ('y', 'both'):
        ax.set_yticks(cos_minor, minor=True)

    ax.grid(True, which='major', alpha=0.1)


def draw_bezier_handle(ax: Axes, cp1: Tensor, cp2: Tensor, *, color: ColorType, handlecolor: ColorType, **kwargs):
    cx, cy = zip(cp1, cp2, strict=True)
    ax.plot(
        cx,
        cy,
        color=color,
        linewidth=1.5,
        zorder=0,
        **kwargs,
    )
    ax.plot(
        cx,
        cy,
        color=color,
        linestyle=' ',
        marker='o',
        markersize=4,
        markerfacecolor=handlecolor,
        markeredgewidth=1.2,
        **kwargs,
    )

Suppression

This type of intervention is used to reduce the magnitude of embeddings that are aligned with a concept vector. There are at least two ways to do that:

• Reduce the overall magnitude of aligned embeddings, without changing their direction
• Reduce the aligned component, without changing unaligned components.

The type implemented here is the second variety. The Suppression intervention selectively reduces the component of activations that align with a target concept:

$$\mathbf{x}' = \mathbf{x} - g(\alpha) \cdot (\mathbf{x} \cdot \mathbf{v}) \cdot \mathbf{v}$$

Where:

• $\mathbf{x} \in \mathbb{R}^E$ are the input activations
• $\mathbf{v} \in \mathbb{R}^E$ is the unit-norm concept vector ($\|\mathbf{v}\|_2 = 1$)
• $\alpha = \max(0, \min(1, \mathbf{x} \cdot \mathbf{v})) \in [0,1]$ is the clamped alignment
• $g(α)$ is the suppression gate strength (see below)
• $\mathbf{x} \cdot \mathbf{v} \in [-1,1]$ is the raw signed projection magnitude used in the suppression

The intervention preserves the components of $\mathbf{x}$ orthogonal to $\mathbf{v}$ while selectively reducing the aligned component based on how strongly the activation aligns with the concept direction.

from typing import override

import torch
from torch import Tensor

from ex_color.intervention.intervention import Intervention, VarAnnotation


class Suppression(Intervention):
    kind = 'linear'

    def __init__(
        self,
        concept_vector: Tensor,  # Embedding to suppress [E] (unit norm)
        falloff: Mapper,  # Function to calculate strength of suppression
    ):
        super().__init__()
        self.concept_vector = concept_vector
        self.falloff = falloff

    @override
    def dist(self, activations):
        dots = torch.sum(activations * self.concept_vector[None, :], dim=1)  # [B]
        return dots.clamp(min=0, max=1)

    def gate(self, activations: Tensor) -> Tensor:
        return self.falloff(self.dist(activations))

    @override
    def forward(self, activations):
        gate = self.gate(activations)
        p = torch.einsum('b...e,e->b...', activations, self.concept_vector)
        return activations - torch.einsum('b...,e->b...e', gate * p, self.concept_vector)

    @property
    @override
    def annotations(self):
        return self.falloff.annotations

    @override
    def annotate_activations(self, activations):
        return VarAnnotation('strength', self.gate(activations))

Bounded falloff

The BoundedMapper class implements a threshold-based falloff function that maps alignment strength to suppression intensity:

$$ g(\alpha) = \begin{cases} 0 & \text{if } \alpha \leq a \\ b \left(\frac{\alpha - a}{1 - a}\right)^p & \text{if } \alpha > a \end{cases} $$

Where:

• $\alpha \in [-1,1]$ is the alignment between activation and concept vector
• $a \in [0,1)$ is the threshold below which no suppression occurs
• $b \in [0,1]$ is the maximum suppression strength
• $p \ge 1$ is the power that controls the falloff curve shape

This creates a smooth transition from no suppression (below threshold $a$) to maximum suppression strength $b$, with the power parameter controlling whether the falloff is linear ($p=1$) or convex ($p>1$).

from annotated_types import Ge, Le
from typing import Annotated, Sequence

from pydantic import validate_call
import torch
from torch import Tensor

from ex_color.intervention.intervention import ConstAnnotation, VarAnnotation


class BoundedMapper:
    @validate_call
    def __init__(
        self,
        a: Annotated[float, [Ge(0), Le(1)]],
        b: Annotated[float, [Ge(0), Le(1)]],
        power: Annotated[float, [Ge(1)]] = 1.0,
        eps=1e-8,
    ):
        self.a = a
        self.b = b
        self.power = power
        self.eps = eps

    def __call__(self, alignment: Tensor) -> Tensor:
        if self.a > 1 - self.eps:
            return alignment

        shifted = (alignment - self.a) / (1 - self.a)
        shifted = shifted**self.power * (self.b)
        return torch.where(alignment > self.a, shifted, torch.zeros_like(alignment))

    @property
    def annotations(self) -> Sequence[ConstAnnotation]:
        return [
            ConstAnnotation('input', 'angular', 'a', self.a),
            ConstAnnotation('output', 'linear', 'b', self.b),
        ]

    def __repr__(self):
        return f'{type(self).__name__}({self.a:.2g}, {self.b:.2g}, {self.power:.2g})'

    def __str__(self):
        components = []
        if self.a != 0:
            components.append(rf'$a={self.a:.2g}$')
        if self.b != 1:
            components.append(rf'$b={self.b:.2g}$')
        if self.power != 1:
            components.append(rf'$p={self.power:.2g}$')
        return ', '.join(components)

from math import cos, pi
from typing import cast, override

import matplotlib.pyplot as plt
from matplotlib.projections.polar import PolarAxes
from pydantic import validate_call

from utils.nb import displayer_mpl
from utils.plt import Theme


falloffs = [
    BoundedMapper(0, 0.5),
    BoundedMapper(0, 0.5, power=2),
    BoundedMapper(cos(pi / 3), 1),
    BoundedMapper(cos(pi / 3), 1, power=2),
]


def _make_fig(theme: Theme):
    n = len(falloffs)
    fig = plt.figure(figsize=(1 + 4.5 * n, 9), layout='compressed')

    axes = []
    linear_axes = []
    lax = None
    for i, mapper in enumerate(falloffs):
        ax = cast(PolarAxes, fig.add_subplot(2, n, i + 1, axes_class=PolarAxes))
        ax.spines['polar'].set_color(c='gray')
        ax.grid(True, color='#444', linewidth=0.5)

        idf = Suppression(
            torch.tensor([1, 0], dtype=torch.float32),  # North
            mapper,
        )
        draw_intervention_slice(ax, idf, theme=theme)
        ax.set_title(str(idf.falloff), pad=15)
        ax.tick_params(labelleft=False)  # The y-axis is actually the radial axis
        ax.spines['polar'].set_visible(False)
        axes.append(ax)

        # Linear suppression-strength chart
        lax = fig.add_subplot(2, n, n + i + 1, sharey=lax)
        draw_suppression_strength(lax, mapper, theme=theme)
        lax.set_aspect('equal')
        lax.set_adjustable('box')
        if i > 0:
            lax.tick_params(labelleft=False)
            lax.set_ylabel('')
            lax.set_xlabel('')
        linear_axes.append(lax)

    # Single legend for all polar axes
    handles, labels = axes[0].get_legend_handles_labels()
    fig.legend(
        handles,
        labels,
        loc='lower center',
        ncol=len(labels),
        frameon=False,
        bbox_to_anchor=(0.5, 0.05),
        bbox_transform=fig.transFigure,
        fontsize='medium',
    )

    fig.suptitle(r' ')
    plt.close(fig)
    return fig


with displayer_mpl(
    f'large-assets/ex-{nb_id}-suppression.png',
    alt_text="Plots of interventions. Top row: semicircular polar plots showing the effects of suppression on activations. Each plot shows two lobes: an orange one indicating the magnitude of the intervention, and a blue one showing the transformed activation space. The direction being intervened on (the 'subject') is always 'up', so the orange 'magnitude' lobes are also oriented upwards. The blue 'transformed' lobes are more circular but have a depression in the top, showing that the directions more aligned with the subject are squashed/attenuated by the intervention. Bottom row: line charts showing intervention strength as a function of alignment.",
    live=False,
) as show:
    # Two rows: polar slices (top) and linear suppression amount (bottom)
    show(_make_fig)

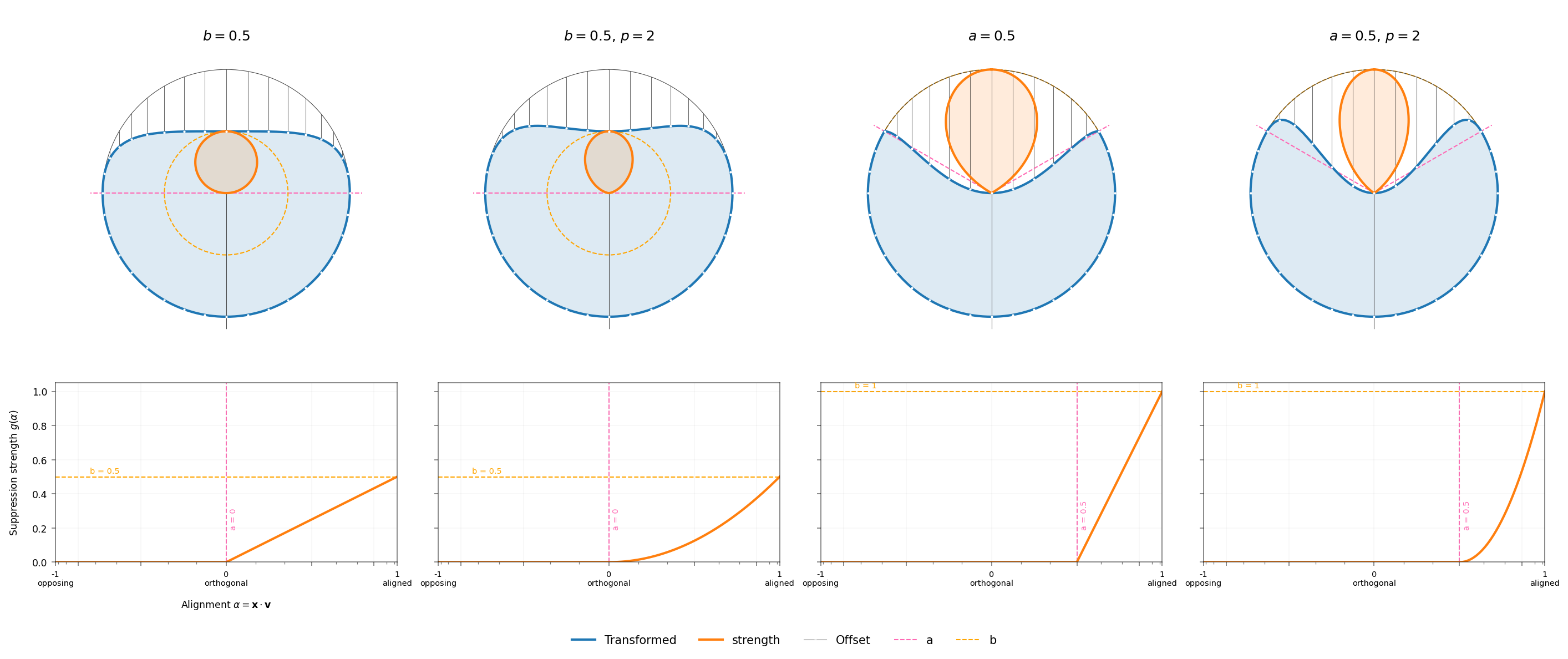
Suppression intervention lobes. Top row: Polar projections where the angular coordinate represents the direction of a unit input vector, and the radial coordinate shows magnitude. The blue filled region shows transformed activations, while the orange region show suppression strength. White lines illustrate the transformation from original to suppressed activations (dots). Bottom row: Suppression strength as a function of alignment.

Repulsion

The Repulsion intervention rotates activations away from a concept vector within their shared 2D plane:

$$\mathbf{x}' = m(\alpha) \mathbf{v} + \sqrt{1 - m(\alpha)^2} \mathbf{u}_\perp$$

Where:

• $\mathbf{x} \in \mathbb{R}^E$ are the input activations (assumed unit norm)
• $\mathbf{v} \in \mathbb{R}^E$ is the unit-norm concept vector
• $\alpha = \max(0, \min(1, \mathbf{x} \cdot \mathbf{v}))$ is the original clamped alignment
• $\mathbf{u}_\perp = \frac{\mathbf{x} - (\mathbf{x} \cdot \mathbf{v})\mathbf{v}}{\|\mathbf{x} - (\mathbf{x} \cdot \mathbf{v})\mathbf{v}\|}$ is the unit vector perpendicular to $\mathbf{v}$ in the plane spanned by $\mathbf{x}$ and $\mathbf{v}$

The intervention only applies to activations with positive alignment ($\mathbf{x} \cdot \mathbf{v} > 0$), leaving others unchanged.

This approach preserves the geometric relationships of a unit norm embedding space: instead of damping components like in suppression, it steers the representation to a new point on the unit sphere. The rotation happens entirely within the 2D plane defined by the original activation and the concept vector, which means the resulting activation vector is as close to the original representation as possible while still being repelled away.

For the edge case where activations are nearly parallel to the concept vector (making $\mathbf{u}_\perp$ ill-defined), our implementation generates a random orthogonal direction using Gram-Schmidt orthogonalisation. This ensures the rotation can still proceed, although this could result in the vector being pushed into an out-of-distribution region. It may make more sense to analyze the representation space beforehand to determine a default direction to use.

The constraint that rotated vectors maintain unit norm emerges naturally from the spherical geometry — any point on the unit sphere can be parameterised by its alignment with a reference direction and its perpendicular component.

from typing import override

import torch
from torch import Tensor

from ex_color.intervention.intervention import Intervention


class Repulsion(Intervention):
    kind = 'rotational'

    def __init__(
        self,
        concept_vector: Tensor,  # Embedding to steer away from [E] (unit norm)
        mapper: Mapper,  # Function to recalculate dot products to determine rotation of activations
        eps: float = 1e-8,  # Numerical stability threshold
    ):
        """
        Repel activations away from subject vector by rotating in their shared plane.

        Returns:
            Rotated activations with unit norm, shape [B, E].
        """
        super().__init__()
        self.concept_vector = concept_vector
        self.mapper = mapper
        self.eps = eps

    @override
    def dist(self, activations):
        dots = torch.sum(activations * self.concept_vector[None, :], dim=1)  # [B]
        return torch.clamp(dots, 0, 1)

    @override
    def forward(self, activations):
        # Calculate original dot products
        dots = self.dist(activations)  # [B]

        # Scale dot products with falloff function
        target_dots = self.mapper(dots)  # [B]

        # Decompose into parallel and perpendicular components
        v_parallel = dots[:, None] * self.concept_vector[None, :]  # [B, E]
        v_perp = activations - v_parallel  # [B, E]

        # Get perpendicular unit vectors (handle near-parallel case)
        v_perp_norm = torch.norm(v_perp, dim=1, keepdim=True)  # [B, 1]

        # For nearly parallel vectors, choose random orthogonal direction
        nearly_parallel = (v_perp_norm < self.eps).squeeze()  # [B]

        if nearly_parallel.any():
            # Generate random orthogonal vectors
            random_vecs = torch.randn_like(v_perp[nearly_parallel])
            # Make orthogonal to subject using Gram-Schmidt
            proj = torch.sum(random_vecs * self.concept_vector[None, :], dim=1, keepdim=True)
            random_vecs = random_vecs - proj * self.concept_vector[None, :]
            random_vecs = random_vecs / torch.norm(random_vecs, dim=1, keepdim=True)

            v_perp[nearly_parallel] = random_vecs
            v_perp_norm[nearly_parallel] = 1.0

        u_perp = v_perp / v_perp_norm  # [B, E]

        # Construct rotated vectors in the (subject, u_perp) plane
        target_dots_clamped = torch.clamp(target_dots, -1 + self.eps, 1 - self.eps)
        perp_component = torch.sqrt(1 - target_dots_clamped**2)  # [B]

        v_rotated = (
            target_dots_clamped[:, None] * self.concept_vector[None, :] + perp_component[:, None] * u_perp
        )  # [B, E]

        # Only apply rotation to vectors with positive original dot product
        should_rotate = dots > 0  # [B]
        return torch.where(should_rotate[:, None], v_rotated, activations)

    @property
    @override
    def annotations(self):
        return self.mapper.annotations

    @override
    def annotate_activations(self, activations):
        dots = self.dist(activations)  # [B]
        target_dots = self.mapper(dots)  # [B]
        return VarAnnotation('offset', (dots - target_dots).abs())

Linear mapper

The LinearMapper creates a piecewise-linear transformation that compresses the upper range of alignment values:

$$ m_{\text{linear}}(\alpha) = \begin{cases} \alpha & \text{if } \alpha \leq a \\ a + (b - a) \cdot \frac{\alpha - a}{1 - a} & \text{if } \alpha > a \end{cases} $$

Where:

• $\alpha \in [0,1]$ is the clamped alignment between activation and concept vector
• $a \in [0,1)$ is the threshold below which no mapping occurs
• $b \in (0,1]$ is the maximum mapped value (with $a < b$)

This effectively brings alignments above threshold $a$ into the range $[a,b]$, creating a "ceiling" effect that prevents activations from becoming too aligned with the concept vector.

from ex_color.intervention.intervention import ConstAnnotation


from annotated_types import Ge, Gt, Le, Lt
from typing import Annotated


class LinearMapper(Mapper):
    @validate_call
    def __init__(
        self,
        a: Annotated[float, [Ge(0), Lt(1)]],
        b: Annotated[float, [Gt(0), Le(1)]],
        eps=1e-8,
    ):
        assert a < b
        self.a = a
        self.b = b
        self.eps = eps

    def __call__(self, alignment: Tensor) -> Tensor:  # alignment is a batch, shape [B]
        shifted = (alignment - self.a) / (1 - self.a)
        shifted = shifted * (self.b - self.a) + self.a
        return torch.where(alignment > self.a, shifted, alignment)

    @property
    def annotations(self):
        return [
            ConstAnnotation('input', 'angular', 'a (start)', self.a),
            ConstAnnotation('output', 'angular', 'b (end)', self.b),
        ]

    def __repr__(self):
        return f'{type(self).__name__}({self.a:.2g}, {self.b:.2g})'

    def __str__(self):
        components = ['Linear']
        if self.a != 0:
            components.append(rf'$a = {self.a:.2g}$')
        if self.b != 1:
            components.append(rf'$b = {self.b:.2g}$')
        return rf'{", ".join(components)}'

Bézier mapper

The BezierMapper implements a cubic Bézier curve to create smooth, controllable mapping functions:

$$\mathbf{B}(t) = (1-t)^3\mathbf{P}_0 + 3(1-t)^2t\mathbf{P}_1 + 3(1-t)t^2\mathbf{P}_2 + t^3\mathbf{P}_3$$

Where the control points are constructed as:

• $\mathbf{P}_0 = (a, a)$ — start point
• $\mathbf{P}_3 = (1, b)$ — end point
• $\mathbf{P}_1, \mathbf{P}_2$ — intermediate control points derived from tangent constraints

The mapping function $m_{\text{bezier}}(\alpha)$ is obtained by:

1. Inverse parameterisation: For input $\alpha > a$, solve $B_x(t) = \alpha$ for parameter $t$
2. Function evaluation: Return $m_{\text{bezier}}(\alpha) = B_y(t)$

The intermediate control points are positioned to satisfy tangent slope constraints:

$$\mathbf{P}_1 = \mathbf{P}_0 + d \cdot (\mathbf{I} - \mathbf{P}_0)$$ $$\mathbf{P}_2 = \mathbf{P}_3 + d \cdot (\mathbf{I} - \mathbf{P}_3)$$

Where:

• $\mathbf{I}$ is the intersection of tangent lines at the start and end points
• $d$ is the control_distance parameter

This construction ensures the curve has the desired start slope (typically 1.0 to match the identity function) and end slope (typically 0.0 for a smooth ceiling effect).

The core challenge is the inverse parameterisation — given $\alpha$, finding $t$ such that $B_x(t) = \alpha$. Our implementation uses Newton's method with automatic differentiation:

$$t_{n+1} = t_n - \frac{B_x(t_n) - \alpha}{B'_x(t_n)}$$

The FastBezierMapper variant trades memory for speed by precomputing a lookup table and using linear interpolation — a trick commonly used in computer graphics.

from math import sqrt

import torch
from torch import Tensor


class BezierMapper(Mapper):
    @validate_call
    def __init__(
        self,
        a: Annotated[float, [Ge(0), Lt(1)]],
        b: Annotated[float, [Gt(0), Le(1)]],
        start_slope: float = 1.0,  # Aligned with unmapped leadup
        end_slope: float = 0.0,  # Flat
        control_distance: float = 1 / sqrt(2),  # Relative to intersection point
    ):
        assert a < b <= 1
        self.a = a
        self.b = b

        # Find intersection of the two tangent lines
        # Line 1: y - a = start_slope * (x - a)  =>  y = start_slope * (x - a) + a
        # Line 2: y - b = end_slope * (x - 1)    =>  y = end_slope * (x - 1) + b
        # At intersection: start_slope * (x - a) + a = end_slope * (x - 1) + b

        if abs(start_slope - end_slope) < 1e-8:
            # Parallel lines - use midpoint as fallback
            intersection_x = (a + 1) / 2
            intersection_y = (a + b) / 2
        else:
            intersection_x = (a * (start_slope - 1) + b - end_slope) / (start_slope - end_slope)
            intersection_y = start_slope * (intersection_x - a) + a

        intersection = torch.tensor([intersection_x, intersection_y], dtype=torch.float32)

        # Define the 4 control points for cubic Bézier
        self.P0 = torch.tensor([a, a], dtype=torch.float32)
        self.P3 = torch.tensor([1.0, b], dtype=torch.float32)

        # P1: distance from P0 towards intersection, scaled by control_distance
        direction_to_intersection = intersection - self.P0
        self.P1 = self.P0 + control_distance * direction_to_intersection

        # P2: distance from P3 towards intersection, scaled by control_distance
        direction_to_intersection = intersection - self.P3
        self.P2 = self.P3 + control_distance * direction_to_intersection

    def bezier_point(self, t: Tensor) -> Tensor:
        """Evaluate cubic Bézier curve at parameter t"""
        one_minus_t = 1 - t

        term0 = (one_minus_t**3)[:, None] * self.P0[None, :]
        term1 = (3 * one_minus_t**2 * t)[:, None] * self.P1[None, :]
        term2 = (3 * one_minus_t * t**2)[:, None] * self.P2[None, :]
        term3 = (t**3)[:, None] * self.P3[None, :]

        return term0 + term1 + term2 + term3

    def bezier_x(self, t: Tensor) -> Tensor:
        """Get x-coordinate of Bézier curve at parameter t"""
        return self.bezier_point(t)[:, 0]  # Changed from [..., 0]

    def bezier_y(self, t: Tensor) -> Tensor:
        """Get y-coordinate of Bézier curve at parameter t"""
        return self.bezier_point(t)[:, 1]  # Changed from [..., 1]

    def solve_for_t(self, x: Tensor, max_iters: int = 10) -> Tensor:
        """Solve for parameter t such that bezier_x(t) = x using Newton's method"""
        # Initial guess: linear interpolation
        t = (x - self.a) / (1 - self.a)
        t = torch.clamp(t, 0.01, 0.99)  # Avoid endpoints

        for _ in range(max_iters):
            # Newton step: t_new = t - f(t)/f'(t)
            # where f(t) = bezier_x(t) - target_x

            # Enable gradients for automatic differentiation
            t_var = t.clone().requires_grad_(True)
            x_pred = self.bezier_x(t_var)
            error = x_pred - x

            # Compute derivative dx/dt
            dx_dt = torch.autograd.grad(x_pred.sum(), t_var, create_graph=False)[0]

            # Newton update (be careful with division by zero)
            dt = error / (dx_dt + 1e-8)
            t = t - dt
            t = torch.clamp(t, 0.0, 1.0)

            # Check convergence
            if torch.max(torch.abs(error)) < 1e-6:
                break

        return t

    def __call__(self, alignment: Tensor) -> Tensor:
        result = alignment.clone()

        # Only apply Bézier mapping for alignment > a
        mask = alignment > self.a
        if mask.any():
            x_vals = alignment[mask]

            # Solve for t parameters
            t_vals = self.solve_for_t(x_vals)

            # Get corresponding y values
            y_vals = self.bezier_y(t_vals)

            result[mask] = y_vals

        return result

    @property
    def annotations(self):
        return [
            ConstAnnotation('input', 'angular', 'start', self.a),
            ConstAnnotation('output', 'angular', 'end', self.b),
        ]

    def __repr__(self):
        return f'BezierMapper(a={self.a:.2g}, b={self.b:.2g})'

    def __str__(self):
        components = ['Bézier']
        if self.a != 0:
            components.append(rf'$a = {self.a:.2g}$')
        if self.b != 1:
            components.append(rf'$b = {self.b:.2g}$')
        return rf'{", ".join(components)}'


class FastBezierMapper(BezierMapper):
    def __init__(self, *args, lookup_resolution: int = 1000, **kwargs):
        super().__init__(*args, **kwargs)

        # Precompute lookup table
        t_vals = torch.linspace(0, 1, lookup_resolution, dtype=torch.float32)
        bezier_points = self.bezier_point(t_vals)

        # Ensure contiguous storage to avoid searchsorted warning
        self.x_lookup = bezier_points[:, 0].contiguous()  # x coordinates
        self.y_lookup = bezier_points[:, 1].contiguous()  # y coordinates

    def interpolate_1d(self, x_query: Tensor) -> Tensor:
        """1D linear interpolation using lookup table"""
        # Find insertion points for x_query in x_lookup
        indices = torch.searchsorted(self.x_lookup, x_query, right=False)

        # Clamp indices to valid range
        indices = torch.clamp(indices, 1, len(self.x_lookup) - 1)

        # Get surrounding points
        x0 = self.x_lookup[indices - 1]
        x1 = self.x_lookup[indices]
        y0 = self.y_lookup[indices - 1]
        y1 = self.y_lookup[indices]

        # Linear interpolation: y = y0 + (y1 - y0) * (x - x0) / (x1 - x0)
        t = (x_query - x0) / (x1 - x0 + 1e-8)  # Add small epsilon to avoid division by zero
        y_interp = y0 + t * (y1 - y0)

        return y_interp

    @override
    def __call__(self, alignment: Tensor) -> Tensor:
        result = alignment.clone()
        mask = alignment > self.a

        if mask.any():
            x_vals = alignment[mask]

            # Use interpolation on lookup table instead of Newton's method
            y_vals = self.interpolate_1d(x_vals)

            result[mask] = y_vals

        return result

from math import cos, pi
from typing import cast

import matplotlib.pyplot as plt
from matplotlib.projections.polar import PolarAxes

falloffs: list[Mapper] = [
    LinearMapper(0, cos(pi / 3)),
    FastBezierMapper(0, cos(pi / 3), end_slope=0.2),
    LinearMapper(cos(pi / 3), cos(pi / 6)),
    FastBezierMapper(cos(pi / 3), cos(pi / 6), end_slope=0.2),
]


def _make_fig(theme: Theme):
    n = len(falloffs)
    fig = plt.figure(figsize=(1 + 4.5 * n, 9.5), layout='compressed')

    axes = []
    linear_axes = []
    lax = None
    for i, mapper in enumerate(falloffs):
        ax = cast(PolarAxes, fig.add_subplot(2, n, i + 1, axes_class=PolarAxes))
        ax.spines['polar'].set_color(c='gray')
        ax.grid(True, color='#444', linewidth=0.5)

        idf = Repulsion(
            torch.tensor([1, 0], dtype=torch.float32),  # North
            mapper,
        )
        draw_intervention_slice(ax, idf, theme=theme)
        ax.set_title(str(idf.mapper), pad=15)
        ax.tick_params(labelleft=False)  # The y-axis is actually the radial axis
        ax.spines['polar'].set_visible(False)
        axes.append(ax)

        # Linear mapping chart using the same mapping function ("falloff" here)
        lax = fig.add_subplot(2, n, n + i + 1, sharey=lax)
        draw_mapping_linear(lax, mapper, theme=theme)
        lax.set_aspect('equal')
        if i > 0:
            lax.tick_params(labelleft=False)
            lax.set_ylabel('')
            lax.set_xlabel('')

        # Control points overlay
        if isinstance(mapper, BezierMapper):
            draw_bezier_handle(
                lax,
                mapper.P0,
                mapper.P1,
                color='hotpink',
                handlecolor=theme.val('white', dark='black'),
            )
            draw_bezier_handle(
                lax,
                mapper.P2,
                mapper.P3,
                color='orange',
                handlecolor=theme.val('white', dark='black'),
            )
        linear_axes.append(lax)

    # Single legend for all polar axes
    handles, labels = axes[0].get_legend_handles_labels()
    fig.legend(
        handles,
        labels,
        loc='lower center',
        ncol=len(labels),
        frameon=False,
        bbox_to_anchor=(0.5, -0.05),
        bbox_transform=fig.transFigure,
        fontsize='medium',
    )

    fig.suptitle(' ')
    plt.close(fig)
    return fig


with displayer_mpl(
    f'large-assets/ex-{nb_id}-repulsion.png',
    alt_text="Plots of interventions. Top row: circular polar plots showing the effects of repulsion on activations. Each plot shows two lobes: an orange one indicating the magnitude of the intervention, and a blue one showing the transformed activation space. The direction being intervened on (the 'subject') is always 'up', so the orange 'magnitude' lobes are also oriented upwards. The blue 'transformed' lobes are more circular but have a chunk taken out of the top, showing that the directions more aligned with the subject are rotated/pushed away by the intervention. Bottom row: line charts of post-intervention alignment as a function of original alignment.",
    live=False,
) as show:
    show(_make_fig)

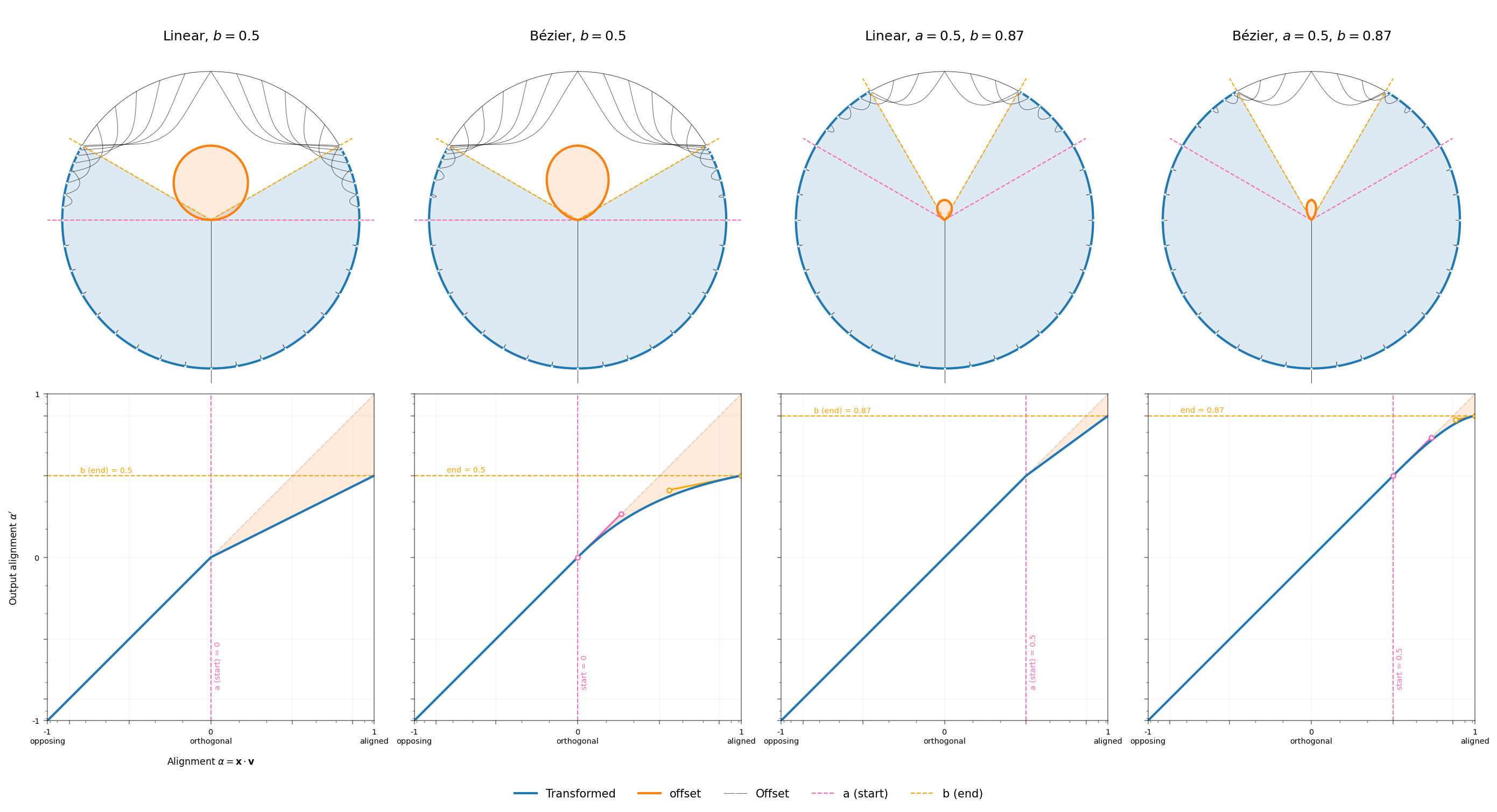
Repulsion intervention lobes. Top row: Polar plots show how vectors are rotated to new positions on the unit sphere, with curved "chord" lines illustrating the rotation paths from input to output positions (white dots). Bottom row: Mapping functions $m(\alpha)$ that determine target alignments. The columns alternate between using linear mappers and Bézier mappers. The filled regions between the identity line and mapping curve indicate the magnitude of alignment reduction.